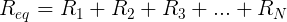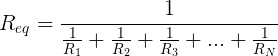T³: Adventures in Science – Series and Parallel Circuits
There are two basic ways to connect electronic components with two terminals: series and parallel. In this episode, we examine those two types of circuits and show how to calculate equivalent resistance.
Most basic electronic components with two terminals, like resistors, can be connected in one of two ways: series or parallel. These connections allow us to mix and match different values of components (or even different components!) to achieve some desired behavior in a circuit.
In the video, we examine how resistors can be connected, and how to calculate the equivalent resistance of each type of circuit.
In a series circuit, components are attached end-to-end and share one common node:
To extend it to more than one resistor, we can calculate the effective resistance (i.e. equivalent resistance) of resistors attached in series by adding up the resistances:
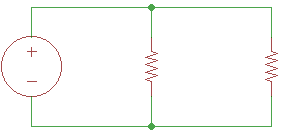
In parallel, components share two common nodes, and current has the option of flowing through one of the components:
From that, we can calculate the equivalent resistance of the resistors attached in parallel by taking the reciprocal of the sum of reciprocal resistances. The following equation has been extended to include any number of resistors:
If you would like a written refresher on what a node is and how to calculate equivalent resistance from series and parallel circuits, we have a written tutorial created by our very own Pete:
That's the fifth and final (for a while) Adventures in Science concept video! Thank you all for the great feedback. I need to work on some other things for the upcoming holiday season, but if we get back around to doing more of these, what other concepts would you like to see covered?
Interested in learning more foundational topics?
See our Engineering Essentials page for a full list of cornerstone topics surrounding electrical engineering.
Good video and explanation. I thought that Liquid Circuitry 2.0 could be confusing if you didn't understand how the pipe valves worked (Handle parallel to flow = ON, handle perpendicular to flow = OFF).
Initially, the fact that the pipe layout didn't match graphically to the written schematics was a little confusing, too. It took me a minute to figure out what was going on.
Personally, I liked the algebra explaining how to arrive at the final formula, but I can see how that could be intimidating. Maybe a "Mythbusters" style "Warning: Science" graphic would help. But in a Sparkfun kind of way. :- )
Resistance is pretty easy. Things get more fun when the mix includes capacitance and/or inductance. Are there some easy ways to analyze some of these cases or does it take Higher Mathematics?
If you're looking to calculate equivalent inductance, the calculations are similar to resistors. For capacitance, it's the opposite. Parallel capacitors add, and you do the summation of reciprocals for series.
Like Member #134773 mentioned, you need some Calculus to analyze how capacitors and inductors behave, as they affect a circuit based on the change in voltage or current.
Actually, you don't need calculus to derive the equations for capacitors. The trick is to use electric charge, not current, and the definition of capacitance, C = Q/V. When the capacitors are connected in parallel, the charge supplied by the source is distributed between the two capacitors, thus Qs = Q1+Q2. When in series, the source pushes a charge into C1 which pushes the same charge into C2 which finally pushes the same charge back to the source, thus Qs = Q1 = Q2. With just a little algebra, the equations are yours.
Note: The calculus buffs would remind us that charge is just the integral of current, so I guess the calculus is there, just hidden!