When I was in seventh grade, my math teacher often deviated from the textbook lessons, trying to instill an intuitive sense of how numbers work. These digressions were probably leftovers of the "new math" concepts from the sixties, and formed the seeds of what is known as numeracy, or numeric literacy.
One of those lessons was how to check for integer divisibility - can we divide an integer number by another, with no remainder? And can we do the check in the time it takes our eye to scan the number, not having to punch it into a calculator or grind out the long division?
As a side note - I didn't know it at the time, but the distinction between integers and fractional numbers becomes pretty significant when you start getting into computer programming - particularly for embedded platforms. On small chips like the AVR (the heart of a RedBoard), the chip has internal hardware that can handle integer math on its own, but its floating point numbers are computed using a software library. Doing floating point calculations is significantly less efficient on the AVR than integer calculation - understanding how to translate a floating point problem into an integer one is a very useful skill!
The divisibility checks broke down something like this for a given integer number:
- Divisible by 1 is trivial - everything is divisible by 1.
- Divisible by 2, 5 and 10 are pretty easy to check using the rightmost digit.
- If the rightmost digit is even (0, 2, 4, 6, or 8), it's divisible by 2.
- If it's 0, it's divisible by 10.
- If it's 0 or 5, it's divisible by 5.
- Divisible by 6 means divisible by both 2 and 3.
- Divisible by 4 means divisible by 2 twice - check for 2, if that passes, divide by 2 and check that.
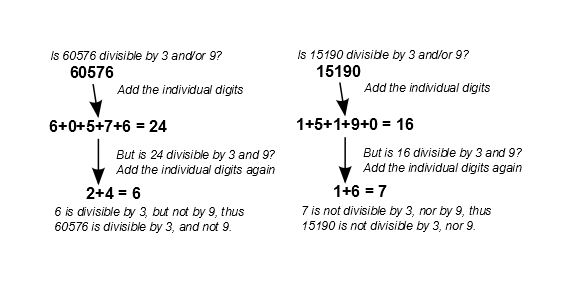
You'll notice that I haven't mentioned the rule for divisibility by three or nine - while the rules above are obvious after you think about them a bit, three is the one that really stuck with me. It's a little more involved, but still quick and intuitive to apply.
- Looking at the digits, add each successive digit.
- If the result is a recognizable multiple of 3 (0, 3, 6, 9, etc.), then then the original number is divisible by 3.
- If the sum is divisible by 9 (0 or 9), the original number is divisible by 9.
- If the first sum is too long to easily recognize, then you can repeat the process, making a second sum that follows the same rules.
She didn't have a good rule for seven - for all of the shortcuts outlined above, divisibility by seven was still the realm of attempting the division and checking the remainder. Beware of prime numbers!
The divisibility by three thing has been an interesting piece of trivia through the years - in preparing to write this, an informal survey of my colleagues revealed that very few of them knew it, a greater number didn't, and one claimed to avoid shortcuts altogether.
Having some casual familiarity with numbers is useful to scientists and engineers. In software and computer engineering, casual familiarity with binary numbers is particularly useful.
Studying computer science in university, a good portion of my sophomore year was spent studying different number systems. I took an introduction to computer architecture class that was a sink-or-swim trial - we really had to be conversant with binary, octal and hex. I remember exams in that class where the instructor would ask us to show our work in the representation of his choosing. We got to be pretty good at doing simple arithmetic in our heads, but it was a great relief when we were allowed to use calculators to handle base conversion.
Binary numbers are the foundation of computing - it's easy to make circuits that are either on or off, and it's easy to gang those circuits up to increase resolution. Binary also quickly becomes cumbersome - an individual bit (or binary digit) doesn't store much information - by the time we've ganged up a bunch of them, the string of on/off indications is unwieldy. If I have 001100010111000000011100, are there 6 or 7 zeros in a row in the middle?
As shorthand, we gather the bits into groups, and use different number bases to describe the groupings:
- Groupings of 3 bits at a time yield values from 0 to 7 - having eight possible codes, we call the result octal, and prefix it with
0cto differentiate it from decimal. - If we make 4-bit groupings, we get 16 possible codes, known as hexadecimal, or hex for short, with the prefix
0x. Since we run out of digits to represent hex values, we pull letters from the start of the alphabet: A, B, C, D, E and F.
In 2015, octal seems anachronistic, and hex has taken over. It's partly a divisibility by three situation: In the age of 32 and 64-bit computers, neither is evenly divisible by 3, though they are divisible by 4. When I was in that architecture class, we were studying the Digital Electronics Corp's PDP-8, which is intrinsically a 12-bit machine - octal and hex were both a part of that landscape.
I'm not really here to get deep into hex - we've got a tutorial that covers it more thoroughly than I can here.
But after years spent thinking (in the shower, while driving my car, riding my bike) about number systems and divisibility by three, I discovered something:
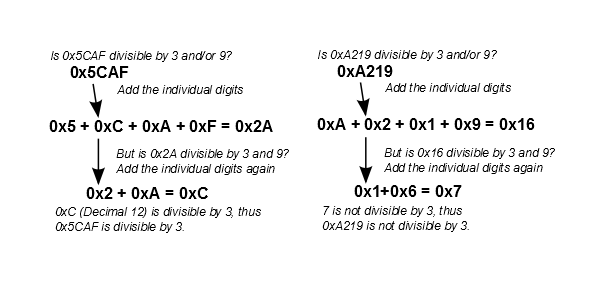
The divisibility-by-three shortcut also works in hexidecimal!
It takes a little bit of adjustment.
- You have to remember to use hex math when adding the digits (0x9 + 0x1 = 0xA, not 10!).
- You need to put 0xC and 0xF (decimal 12 and 15, repsectively) in the list of recognized multiples of three.
So let's examine how this works:
This may also be another reason to use hex instead of octal - octal doesn't follow the sum-of-digits shortcut!
Time will tell how useful this actually is. Computers are pretty deeply based on powers of two, so division by those numbers is much more easily applied, to such a degree that those numbers are frequently used as design specifications (RAM size is based on powers of 2, for example), where multiples of three are not. Still, it's an interesting piece of trivia. Maybe you'll find it useful sometime, if as nothing more than a geeky party trick.
Footnotes
In researching this posting, I've discovered that Wikipedia has a comprehensive list of tests of divisibility for every divisor between 1 and 20.
Additionally, John D. Cook seems to have beat me to this realization, and offers a more complete set of rules for divisibility in hex.






To show divisibility by 7, take all the digits except the rightmost, multiply that number by 3, and add the rightmost digit. Repeat until the number is recognizably divisible by 7.
Example: 42 - multiply 4 by 3 and add 2, you get 14. Multiply 1 by 3 and add 4 to get 7.
Example: 105 - multiply 10 by 3 and add 5 to get 35. Multiply 3 by 3 and add 5 to get 14.
This method occurred to me in 3rd grade. I've attempted a mathematical proof a few times but haven't succeeded. (I don't know how to apply the fact that something pertains only to integers, and not to reals, in a proof.)
I couldn't prove it, but I was able to generalize it: to find if a number is divisible by a number, n, less than ten, take the upper digits, multiply them by (10 - n) and add the rightmost digit.
The key here is that you are taking your number N and breaking it down into two numbers a and b such that N = 10a+b. If you work mod 7, this becomes
N = 10a + b (mod 7) N = (7+3)a + b (mod 7) N = 7a + 3a + b (mod 7) N = 3a + b (mod 7)
So 3a+b gives the same remainder divided by 7 as N, and that's your procedure.
The same reasoning shows why it works for any divisor less than ten. In particular, it shows why the casting out 9's procedure works (or, why in octal, the casting out 7's procedure works for divisibility by 7).
We can also show why the divisibility rule for 3 works:
N = 10a+b (mod 3) N = (33+1)a + b (mod 3) N = (33)a + a + b (mod 3) N = a + b (mod 3)
so N and a+b have the same remainder, mod 3. So you can just add the final digit to the others to get a smaller number with the same remainder, etc.
It's also generalizable to other bases and divisors: In base B, choose n such that n divides B-1 (so B = kn+1 for some k):
N = aB + b (mod n) N = a(kn+1) + b (mod n) N = akn + a + b (mod n) N = a + b (mod n)
So the "sum the digits" rule works for divisibility tests in hexadecimal for 3, 5, and 15 (the divisors of 15).
More generally, if B = kn+l, then the rule becomes "multiply a by l, then add b"
This is the best explanation of this procedure I've seen.
You make it look so easy <blush>.
Thank you for the interesting topic. I've learned and forgotten much of this over the years. In particular I enjoyed the comments about the generalization of the method that @Blaise Pascal posted.
Something that caught my eye however was the third paragraph about the utility of integer math on small embedded controllers; this is probably worth an enginursday blog. I wanted to only use floating point when I started out programming PICs but was enlightened by my mentor of how to use integer math instead. After a while it became second nature. When I began to use compilers instead of assembly language, I still applied integer math and still do even though the compiler provided floating point libraries and my simple programs on large PIC32 chips had room and speed for floating point. Nothing religious here, it's just a way of seeing and solving problems. Horses for courses.
Totally agree. Using integers instead of floating point is one of the best things that you can do to make your code faster, portable and more reliable. In every control system I've programmed, the data comes in as an integer count value from an ADC converter, or as a digital bit value. Nothing comes in floating point. Newbies are eager to immediately turn it into floating point engineering units, not realizing that they are introducing inaccuracies and slowing everything down.
Some may argue that using floating point constants in source code makes it easier to understand. The same can be accomplished with symbolic constants that are defined to have the appropriate integer or scaled integer value.
For the actual control logic, the cleanest data flow is to take the integer data from the ADC, process it in the integer domain, put the result out as an integer to the DAC and only convert it to floating point for display.
If fractions are needed, there's scaled integer.
I know I'm a bit late to the discussion, but there's a trick to the division-by-7 thing, too.
It requires that you memorize 1/7th as a decimal, which is 0.142857 (repeating all six post-decimal digits). Do integer division, then the decimal fraction is always the rotating sequence of those digits, starting with the n-th largest of the digits, where "n" is the integer remainder. So R1 is +0.142857, R2 is +0.285714, R3 is +0.428571, R4 is +0.571428, R5 is +0.714285, R6 is +0.857142. So as long as you can remember the set {1,4,2,8,5,7} and can non-destructively re-sort the set into ascending order, you can divide by 7.
About Octal ... Octal was popular in instruction sets that were based on groups of 3. This was useful when symbolic debuggers were not available, screens were small, printers were slow. Using a PDP-11 Reference card (which was necessary for the same reasons) - here are examples. It had eight registers, so that was a single octal digit in an instruction. There were eight "modes" such as auto increment, "Deferred", use as an address, index (use with a constant added to the register). "Deferred" was an odd value, not deferred was even. So the Clear or Clr instruction was 00 50 MR, in octal defining the mode or use of the register, then the register. Mov was 01 SS DD with the mode and register defined in the respective octal digits. For "banging two stones together" - it was very convenient and an experienced assembly language programmer could read an octal dump as easily as a not commented page of code. There were even certain "gambits" of coding which could be recognized, so one could figure things out just by using bit switches on the front panel and cycling through the memory one word at a time.
Great discussion, however, I avoid division when multiplication can perform the same job, and much faster. eg. dividing by 3 is the same as multiplying by 1/3 = 0.330 or your equivalent scaled integer fraction. eg. dividing by 5 is the same as multiplying by 1/5 = 0.200 or your equivalent scaled integer fraction. eg. dividing by 7 is the same as multiplying by 1/7 = 0.142 or your equivalent scaled integer fraction. This works great when the multiplier is a constant which can be calculated with a calculator, as you write your code. If your original divisor is only known at runtime, then it becomes more of a job to calculate your scaled integer multiplier. You can get away without division in a lot of cases. Perhaps you all already know this, but then again, maybe not. Cheers
Love math and tricks likes this. However, way back in my High School days, we had access to an old Univac Solid State 90.... it used Bi-Quinary coding. 5.4.2.1 Somehow I dont think the tricks would work so well with that. ;)
If you like that, you'll like the cube root trick: you can quickly determine the cube root of any two digit number that has been cubed by looking at the first 3 digits and the last digit of the answer. I'll leave it to the reader to figure out how.
I loved division by 9. You sum the digits and see if that's divisible by 9. The cool thing about it is that this is fully generalizable to any base. So if you have base n, you can do divisibility by n-1 by summing the digits in base n.
Divisibility by 7? Take your number in octal and sum the digits. If the resulting number is divisible by 7, the original number was divisible by 7.
When I was in 7th grade, we learned the easy division rules and the teacher had them up on a bulletin board. For 7 there was a '?'. After I had worked this method out, I made a point to find out if she was still working in the district (she was) and sent her a letter with my results.
I didn't know division by 9 worked like that. It makes sense though because division by 3 works the same way..
Back in 7th grade I was arguing with a friend what was more elegant; hex or octal. After he pointed out that after memorizing the binary representation of the 8080A instruction set, for the move, add, compare, etc, instructions, some of 3 bit fields (which can easily be represented in octal) always map to the same register. Oh, and using a 7447 TTL chip to represent a hex number on a 7 segment display just looked stupid.... couldn't argue with that. - Steve
Nice post, I've been teaching my daughter the divisible by 3 trick.
One minor point. I think the PDP-8 was made by Digital Equipment Corp. (not Digital Electronics Corp).
I knew I shoulda just said "DEC!"
I actually remember learning this in school at some point as well. I specifically remember the teacher saying that there is a method for 7, but it's easier to just divide it out. It always bothered me that I never knew how that one worked. As for 4 and 8 you just need to check that the last 2 or 3 numbers are divisible by 4 or 8 respectively, no need to divide your number by 2.
How do you effectively use this to your advantage with programming? All of these "test" take instruction time, correct?
You could still possibly come out ahead since the architecture doesn't natively support integer division. For instance: you don't need to actually sum the digits repeatedly. You can sum them once, mod 3:
This probably gives you a faster "x % 3" than you'd get from the compiler (it depends on how heavily it optimizes cases where the divisor is known at compile time), but the trade-off is that you are using more code space to do it. Like many optimizations, it becomes a question of how badly you need this one specific operation to be fast. (The above method could also be used for mod 7, by taking three bits at a time, or mod 15, by taking four bits at a time, and adjusting the switch statement accordingly)
On an architecture with integer division implemented in hardware, it's less likely the above method would be worth using. But on AVR it should be faster than an actual division algorithm - the switch statement could be implemented as a jump table, so the whole thing would take roughly 35 instruction cycles per hex digit, and probably a couple hundred bytes of instruction storage.
These tests are actually pretty cumbersome to implement in code, since you've have to convert numbers to strings, then cycle through the strings to compose the sums. Unless you're working in COBOL, where numbers are intrinsically strings, it's not terribly efficient.
Where it is efficient is in the programer's brain while designing and debugging software. If you need to recognize particular multiples, it's easier if you can just "see" them, than to have to pull out a calculator.
The thing it does help with is that you can occur in the programmer's noggin
Worth note that for the hex and octal versions of these, iterating over the digits in the number is as simple as doing i>>=3 or i>>=4 and i & 0xF or i & 0x7 - which is basically the same cost as the string conversion, but without the memory penalty and you're already at linear in the number of digits, and shifts and bitwise-and are usually cheap.
In figure 2, you conclude
I believe you meant to say the opposite, because 0x5CAF is indeed divisible by 3, it becomes 0x1EE5.
Yup - you're right. Now fixed.
I cloned & mutated the decimal figure to make the hex. I remembered to change all the numbers, but forgot the text.
To tie together two of the difficult patches in this article... If you sum the octal digits and get a number divisible by 7, then the original number is divisible by 7.
For example, 1015 (decimal) = 01767 in octal, and 01+07+06+07 = 025 (octal), and 02+05 = 07 (octal), so 01767 (octal) (or 1015 decimal) is divisible by 7. Which it is. 442 decimal is 0672, and 6+7+2 = 017 (octal), which reduces to 1+7 = 010 (octal), which is not divisible by 7, so 442 is not divisible by 7.